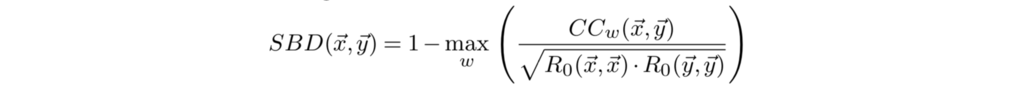最近ある時系列データの因果関係が分析できればと、手始めに時系列データの相関解析やクラスタリングの手法を調査しています。 今回は、時系列データクラスタリング手法の動向と、2015年に論文が発表された正規化相互相関手法を用いた形状ベース(Shape-based)の時系列クラスタリング手法であるk-Shape[3]についてまとめてみます。 クラスタリングとは? クラスタリングとは、対象となるグループに対する高度な知識がなくとも、類似のデータを関連するグループや同種のグループに分割するデータマイニングの手法です。クラスタリングは、科学的データの探査、情報検索とテキストマイニング、CRMやマーケティング、医療診断などの、データマイニングの手法として実用的に用いられています [1]。 研究的な観点からも、クラスタリングは、統計、パターン認識、機械学習などの分野で、現在も活発に研究されています。機械学習的な観点では、クラスタリングは一般的には教師なし学習であり、クラスタリングは、多様な属性を持つ膨大なデータセットを分類したり、潜在するパターンの発見に役立ちます[1] [2]。 k-meansとは k-means(k-平均法)は、現在、科学および産業分野で最も広く使用されているクラスタリングアルゴリズムです。名称は、クラスタの平均(または加重平均)を用いてk個のクラスタに分類する手法に由来しています[3]。 クラスタリングにおいて、すべての可能な組み合わせを確認することは計算上実行不可能(NP困難)な問題です。k-meansは、貪欲法的に局所的最適解を求めて、それを反復して最適化する手法です。 具体的には、k-meansは対象データを表す点を、最初にランダムにk個のクラスタに割り当てます。各クラスタに含まれる点の平均を計算した後に、各クラスタのメンバーが不変になるまで、以下の2つのステップを反復して実行します。 STEP1 : 各対象データを、その重心に最も近い重心のクラスタに移動 STEP2 : 各クラスタの平均を再計算 反復による最適化は、各クラスタのメンバーに移動がなくなり収束した場合、または最大反復回数に達した場合に終了します。 時系列クラスタリングとは クラスタリングの手法は、時系列データの解析にも用いられており、主に時系列データセット内の潜在的、興味深いパターンの発見に利用されます。解析事例としては、株価などの時系列間の相関検出、天気予報などの関数近似と組み合わせた予測、店舗などのアイテム間の関連性の検出などがあります [2]。 時系列クラスタリングの手法 時系列クラスタリング手法を大別すると、モデルベース(Model-based)、特徴ベース(Feature-based)、形状(Shape-based)ベース手法および、その組み合わせの手法に大別されます。以下の図に、各手法に用いられるコンポーネントを示します [2]。 モデルベース(Model-based) モデルベースの手法は、時系列データを対象のモデルデータのパラメータに変換し、モデルで定義されている距離関数および(通常は従来の)クラスタリングアルゴリズムにを用いています。一般的に、モデルベースの手法はクラスタが接近している場合に性能が劣化するなど、スケーラビリティの問題が指摘されています [2]。 特徴ベース(Feature-based) 特徴ベースの手法は、時系列データが低次元の特徴ベクトルに変換され、、従来のクラスタリングアルゴリズムが適用されます。一般的に特徴ベクトルは正規化されており、ユークリッド距離などを用いたクラスタリング手法が用いられます [2]。…
時系列データクラスタリングとk-Shape